12 min to read
风险价值模型、Markowitz模型原理简介及python实现
风险价值模型
概念
风险价值(Value at Risk, VaR),是给定置信水平和目标时段下预期的最大损失,即在市场正常波动的条件下、在一定的概率水平$\alpha%$下,某一金融资产或金融资产组合的$\mathit{VaR}(\alpha,\Delta t)$是在未来特定的一段时间内$\Delta t$的最大可能损失,数学表达式为:
$$ Pr{X_t<-VaR(\alpha,\Delta t)}=\alpha% $$
实操
import numpy as np
import pandas as pd
import tushare as ts
import pyecharts as pye
import seaborn as sns
#读入美的“000333”2017-01-01 到 2018-11-08复权后数据
df = ts.get_h_data('000333', start='2017-01-01', end='2018-11-8')
#其他获取股票数据的方法
'''
start_date='01-07-2015'
end_date='01-07-2017'
united=quandl.get('WIKI/UAL',start_date=start_date,end_date=end_date)
america=quandl.get('WIKI/AAL',start_date=start_date,end_date=end_date)
'''
#计算日均收益率
df1 = df['close'].sort_index(ascending=True)
df1 = pd.DataFrame(df1)
df1['date'] = df1.index
df1['date'] = df1[['date']].astype(str)
df1["rev"]= df1.close.diff(1)
df1["last_close"]= df1.close.shift(1)
df1["rev_rate"]= df1["rev"]/df1["last_close"]
df1 = df1.dropna()
print(df1.head(10))
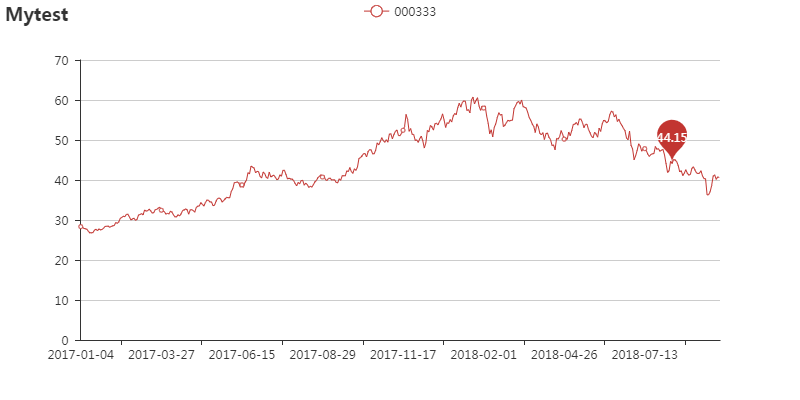
#使用PYECHARTS,画出收盘价曲线
line = pye.Line(title="Mytest")
attr = df1["date"]
v1 = df1["close"]
line.add("000333", attr, v1, mark_point=["average"])
line.render("Line-High-Low.html")
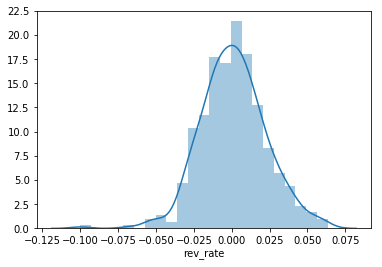
sns.distplot(df1["rev_rate"])
sRate = df1["rev_rate"].sort_values(ascending=True)
p = np.percentile(sRate, (1, 5, 10), interpolation='midpoint')
print(p)
from scipy.stats import norm
u = df1.rev_rate.mean()
σ2 = df1.rev_rate.var()
σ = df1.rev_rate.std()
Z_01 = norm.ppf(0.01) # stats.norm.ppf正态分布的累计分布函数的逆函数,即下分位点
#因为(R* - u)/σ = Z_01
#所有R* = Z_01*σ + u
print( u+Z_01*σ )
结果
Markowitz模型
原理
如果投资人的效用水平仅与财富状况相关,个人投资决策的出发点是为了最大化效用,则投资决策的数学表达式:
$$ \mathop{max}\limits_{\omega_i} \mathbb{E}[U(R_p)]=\mathbb{E}[U(\sum_{i=1}^{N}\omega_i R_i)]\ s.t. \sum_{i=1}^{N}\omega_i=1 $$
假设$R_i,R_2,...,R_N$均服从正态分布,且投资人的效用函数$U(.)$是常见的凹函数,则投资人的上式可以简化为:
$$ \mathop{min}\limits_{\omega_i}\sigma^2(R_p)=\sum_{i=1}^{N}\omega_i^2\sigma^2(R_i)+\sum_{i\neq j}\omega_i\omega_j\sigma(R_i,R_j)\ s.t. \bar{R}p=\sum{i=1}^{N}\mathbb{E}(R_i)\ \sum_{i=1}^{N}\omega_i=1 $$
其中$\bar{R}_p$为投资人的投资目标,公式表明,投资人的资产分配原则是在达成投资目标的前提下,要将投资组合的风险最小化。
整个数学形式是二次规划问题,可以用拉格朗日方法求解。最终的投资比重最优解形式满足:
$$\omega^*=a+b\bar{R}_p$$
其中$a$和$b$与$N$中资产收益率的期望值、方差、协方差有关。决策量的最优解$\omega^*$与投资目标$\bar{R}_p$呈线性关系,而风险水平$\sigma^2(R_p)$是$\omega$的二次函数形式,因此当达到最优解时,风险水平$\sigma^2(R_p)$是投资目标$\bar{R}_p$的二次函数形式。
如果将无风险资产考虑进投资组合,无风险资产的效率前缘恰好与忽略无风险资产的效率前缘相切。如果所有投资人对各资产未来收益率的估计是一致的,那么理性投资人持有风险资产的相对比例应该是一样的,风险偏好水平不同只会影响到持有无风险资产的比例。每个投资人持有的相同的相对投资比例的风险资产组合即为市场投资组合(Market Portfolio),即切点对应的投资组合,此时的投资比例为$\omega_m$,收益率为$R_m$。市场投资组合与无风险资产之间的连线成为资本市场线(Capital Market Line)。由此可以得到资本资产定价模型(Capital Asset Pricing Model, CAPM)。
$$ \mathbb{E}(R_q)=R_f+\beta_{qm}[\mathbb{E}(R_m)-R_f] $$
其中$\beta_{qm}$为资本组合或单一资产与市场投资组合收益率之间的协方差。
实操
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tushare as ts
import scipy.optimize as sco
import scipy.interpolate as sci
from scipy import stats
#获取数据
sharesID=['000651','600519','601318','000858','600887','000333','601166','600036','601328','600104']
shares=pd.DataFrame()
for i in range(10):
df = ts.get_h_data(sharesID[9], start='2017-01-01', end='2017-12-31') #前复权
shares=pd.merge(shares,df['close'].to_frame(),how="outer",left_index=True, right_index=True)
shares.columns =['000651','600519','601318','000858','600887','000333','601166','600036','601328','600104']
shares=shares.dropna()
shares.to_excel('stock_data.xlsx')
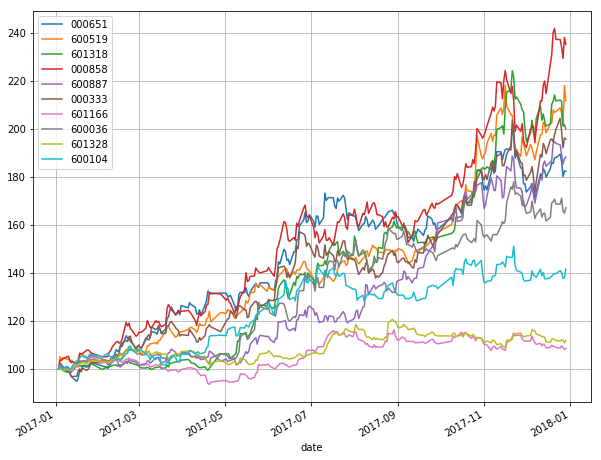
#初步统计
(shares / shares.ix[0] * 100).plot(figsize=(10, 8), grid=True)
log_returns = np.log(shares / shares.shift(1))
np.log(shares / shares.shift(1)).hist(bins=50, figsize=(12, 9))
###投资组合优化
rets = log_returns
number_of_assets = 10 #共有10支股票
portfolio_returns = []
portfolio_volatilities = []
for p in range (10000):
weights = np.random.random(number_of_assets)
weights /= np.sum(weights)
portfolio_returns.append(pow(np.sum(rets.mean() * weights) +1,244)-1)
portfolio_volatilities.append(np.sqrt(np.dot(weights.T,np.dot(rets.cov() * 252, weights))))
portfolio_returns = np.array(portfolio_returns)
portfolio_volatilities = np.array(portfolio_volatilities)
#绘图
plt.figure(figsize=(9, 5)) #作图大小
plt.scatter(portfolio_volatilities, portfolio_returns, c=portfolio_returns / portfolio_volatilities, marker='o') #画散点图
plt.grid(True)
plt.xlabel('expected volatility')
plt.ylabel('expected return')
plt.colorbar(label='Sharpe ratio')
def statistics(weights):
#根据权重,计算资产组合收益率/波动率/夏普率。
#输入参数
#==========
#weights : array-like 权重数组
#权重为股票组合中不同股票的权重
#返回值
#=======
#pret : float
# 投资组合收益率
#pvol : float
# 投资组合波动率
#pret / pvol : float
# 夏普率,为组合收益率除以波动率,此处不涉及无风险收益率资产
#
weights = np.array(weights)
pret = pow(np.sum(rets.mean() * weights) +1,244)-1
pvol = np.sqrt(np.dot(weights.T, np.dot(rets.cov() * 252, weights)))
return np.array([pret, pvol, pret / pvol])
#最大夏普率
def min_func_sharpe(weights):
return -statistics(weights)[2]
bnds = tuple((0, 1) for x in range(number_of_assets))
cons = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
opts = sco.minimize(min_func_sharpe, number_of_assets * [1. / number_of_assets,], method='SLSQP', bounds=bnds, constraints=cons)
opts['x'].round(3) #即为最大夏普率的投资组合的权重分配
statistics(opts['x']).round(3) #获得最大夏普率的投资组合的收益率、波动率和夏普率
#最小方差的投资组合
def min_func_variance(weights):
return statistics(weights)[1] ** 2
optv = sco.minimize(min_func_variance, number_of_assets * [1. / number_of_assets,], method='SLSQP', bounds=bnds, constraints=cons)
statistics(optv['x']).round(3)
##有效边界
def min_func_port(weights):
return statistics(weights)[1]
target_returns = np.linspace(0.10, 1.20, 110)
target_volatilities = []
for tret in target_returns:
cons = ({'type': 'eq', 'fun': lambda x: statistics(x)[0] - tret},
{'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
res = sco.minimize(min_func_port, number_of_assets * [1. / number_of_assets,], method='SLSQP',
bounds=bnds, constraints=cons)
target_volatilities.append(res['fun'])
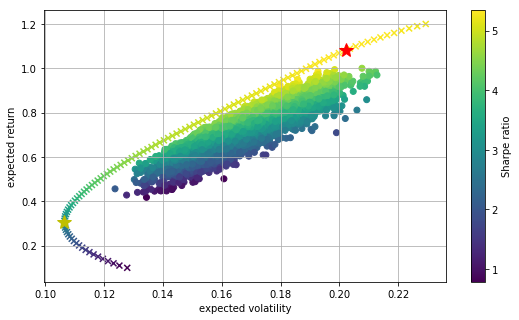
#画散点图
plt.figure(figsize=(9, 5))
plt.scatter(portfolio_volatilities, portfolio_returns,
c=portfolio_returns / portfolio_volatilities, marker='o')
plt.scatter(target_volatilities, target_returns,
c=target_returns / target_volatilities, marker='x')
plt.plot(statistics(opts['x'])[1], statistics(opts['x'])[0],
'r*', markersize=15.0)
plt.plot(statistics(optv['x'])[1], statistics(optv['x'])[0],
'y*', markersize=15.0)
# minimum variance portfolio
plt.grid(True)
plt.xlabel('expected volatility')
plt.ylabel('expected return')
plt.colorbar(label='Sharpe ratio')
##资本市场线
ind = np.argmin(target_volatilities)
upper_half_volatilities = target_volatilities[ind:]
upper_half_returns = target_returns[ind:]
tck = sci.splrep(upper_half_volatilities, upper_half_returns) #插值,使曲线光滑
#tck参数用于构造有效边界函数f(x)
def f(x):
#有效边界函数 (样条函数逼近).
return sci.splev(x, tck, der=0)
#同时也构造有效边界函数f(x)的一阶导数函数df(x)
def df(x):
#有效边界函数f(x)的一阶导数函数
return sci.splev(x, tck, der=1)
def equations(p, risk_free_return=0.02): #参考[4]
eq1 = risk_free_return - p[0]
eq2 = risk_free_return + p[1] * p[2] - f(p[2])
eq3 = p[1] - df(p[2])
return eq1, eq2, eq3
opt = sco.fsolve(equations, [0.01, 0.50, 0.15])
plt.figure(figsize=(9, 5))
plt.scatter(portfolio_volatilities, portfolio_returns,
c=(portfolio_returns - 0.02) / portfolio_volatilities, marker='o')
plt.plot(upper_half_volatilities, upper_half_returns, 'g', lw=4.0)
#设定资本市场线CML的x范围从0到0.6
cml_x = np.linspace(0.0, 0.25)
#带入公式a+b*x求得y,作图
plt.plot(cml_x, opt[0] + opt[1] * cml_x, lw=1.5)
#标出资本市场线与有效边界的切点,红星处
plt.plot(opt[2], f(opt[2]), 'r*', markersize=15.0)
plt.grid(True)
plt.axhline(0, color='k', ls='--', lw=2.0)
plt.axvline(0, color='k', ls='--', lw=2.0)
plt.xlabel('expected volatility')
plt.ylabel('expected return')
plt.colorbar(label='Sharpe ratio')
##置信区间
opt_weights = opts['x'].round(3) # opt_weights是最优风险组合权重
actual_opt_portfolio_returns = np.sum(rets * opt_weights, axis=1) #axis=1 是按行求和 一行中的每一列相加
seven_day_year_returns = np.power(((actual_opt_portfolio_returns.shift(7) + actual_opt_portfolio_returns.shift(6) + actual_opt_portfolio_returns.shift(5) + actual_opt_portfolio_returns.shift(4) + actual_opt_portfolio_returns.shift(3) + actual_opt_portfolio_returns.shift(2) + actual_opt_portfolio_returns.shift(1)) / 7+1),242)-1
seven_day_year_returns = seven_day_year_returns.dropna()
confidence_range = stats.t.interval(0.99, len(seven_day_year_returns)-1, np.mean(seven_day_year_returns), stats.sem(seven_day_year_returns))
结果

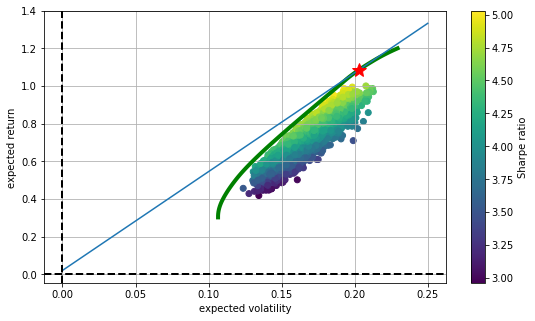
参考资料
[01]. 最优风险资产组合-Python笔记
[02]. Historical Volatility Calculation
[03]. 利用Black-Litterman模型构建投资组合
[04]. [Python for Finance, Statistics, Portfolio Optimization]

Comments